Permeabilidad relativa

A continuación se introduce el concepto de curvas de permeabilidad relativa (KR), a través de un modelo geométrico simple, el cual permite obtener una visión directa de muchos de los principales factores que influyen sobre estas curvas (caudal, gravedad, mojabilidad, heterogeneidad, etc).
El modelo geométrico puede visualizarse como un bloque de sección cuadrada con agujeros cilíndricos longitudinales de extremo a extremo. Estos orificios no se entrecruzan y representan un modelo simplificado de red poral. En los gráficos presentados sólo se muestra una sección cuadrada correspondiente a un corte cualquiera, perpendicular al eje longitudinal del bloque.
Para desarrollar la sección numérica (indispensable para obtener valores de permeabilidad relativa) es conveniente recordar que:

· El área empleada en la fórmula de Darcy corresponde al área global ("bulk") del sistema en estudio.
· El volumen de los capilares cilíndricos (conductos), crece con el cuadrado del radio, puesto que la longitud es constante y el área depende del cuadrado del radio.
VP = ¶ r2 L (Volumen del Capilar)
· La capacidad de conducir fluidos de los capilares cilíndricos (conductos), crece con la cuarta potencia del radio.
Q = ¶ r4 P / (8 μ L) (Ley de Poiseuille)

Si en un bloque se comienza a desplazar el petróleo con agua, asumiendo que no existen fases residuales (conforme al modelo de capilares uniformes), el sistema conducirá ambas fases de acuerdo con los capilares ocupados por cada una de ellas.

Primer Caso: Desplazamiento a bajo caudal con mojabilidad al agua
En este caso la mojabilidad al agua garantiza que el agua invade en primera instancia los capilares más pequeños y progresivamente los medianos como se observa en la Figura 1. Finalmente se calculan las saturaciones y permeabilidades, y representando gráficamente estos cálculos se obtiene la curva de Permeabilidad relativa de la Figura 2.

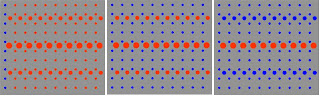Figura 1. Secuencia de la invasión de los capilares con agua

Figura 2. Curva de KR con caudales bajos y mojabilidad al agua

Como se observa en el gráfico, durante el llenado de los capilares más finos, crece la saturación de agua sin incrementar, apreciablemente, la capacidad de conducir este fluido. Recién cuando comienzan a llenarse los capilares de mayor diámetro, el agregado de agua comienza a afectar notablemente la capacidad de conducir petróleo.

Segundo Caso: Mojabilidad al Petróleo
En este caso ocurre lo inverso,los primeros capilares de mayor diámetro son los primeros en ser invadidos por agua, resultando la gráfica de la Figura 3.

Figura 3. Sistema mojable al petróleo

Tercer Caso: Llenado Gravitacional
La invasión con agua se produce siguiendo el ordenamiento vertical de las capas. La forma de la curva (Figura 4) refleja el ordenamiento de las capas.

Figura 4. Llenado con predominio de las Fuerzas Gravitacionales

Cuarto Caso: Llenado Gravitacional con distribución al azar de las capas
En este caso el modelo del medio poroso tiene los poros distribuidos al azar. De esta manera, en cada etapa se inundan poros pequeños, medianos y grandes en la misma proporción que se encuentran en el modelo. Cuando se ha invadido el 25 % de los poros, la fase acuosa alcanzó el 25 % de su conductividad máxima y el petróleo perdió el mismo 25 % (Figura 5).


Figura 5. Predominio gravitatorio con capilares distribuidos al azar

Conclusiones

1.- Si bien la porosidad y la permeabilidad son propiedades del medio poroso, la permeabilidad relativa no lo es.
2.- Las curvas de KR dependen fuertemente de los mecanismos de producción.
3.- Los valores de saturación y permeabilidad en los puntos extremos de las curvas KR son independientes del mecanismo de desplazamiento. (En los sistemas reales ésta es sólo una aproximación al comportamiento físico).

Bibliografía:

Oil Production. http://www.oilproduction.net/files/permeabilidad%20relativa.pdf. Consultado el 07 de octubre de 2008. Autor: M. Crotti. (Última modificación - 18 de junio de 2001).